Robert method

This is another approach closely related to the Findley criterion. The implementation in PragTic was initiated by reports of Kenmeugne et al. in [KVRB96] and [VKRB96], where it can be found together with another proposal for an integral criterion (later found to be Fogue ’s method), in order to compare results of very similar damage parameters but with different computational philosophy. The critical plane criterion is defined as:

The criterion is a maximum damage criterion, thus the result is obtained through maximization of the left-hand side. The resemblance to Findley criterion is clear after a short inspection. The same conditions must be fulfilled under fully reversed loadings and thus:

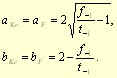
The last unknown parameter has to be set from one test value of repeated bending, i.e.:

The final formula is not correctly reported in [KVRB96], because the two last summands are written there with opposite signs. The report of Kenmeugne et al. [KVRB96] gives only a very vague description of obtained results. PhD theses of Bastien Weber [Web99] and Jan Papuga [Ppg05] show its results in comparison to other methods as very good. The overall ranking in the FatLim Database had been very good as well until the experiments of Bomas et al. [BKL06] were introduced there.

Nomenclature:

Mark	Unit	PragTic variable	Meaning
	[MPa]		shear stress amplitude on an examined plane
	[MPa]	TENS-1, BEND-1	fatigue limit in fully reversed axial loading
	[MPa]	TENS0, BEND0	fatigue limit in repeated axial loading
	[-]		ratio of fatigue limits ()
	[MPa]		amplitude of normal stress on the plane examined
	[MPa]		mean (average value of maximum and minimum values) normal stress on the plane examined
	[MPa]	TORS-1	fatigue limit in fully reversed torsion

Methods & Options & Variables of Calculation – Edit

Decomposition

- Whole load path

Elasto-plasticity

- No – currently no option implemented

Solution option

- Searched planes <0~BS algorithm, 1~globe analogy, 2~random>

- Number of scanned planes

- Optimize <1~yes, 0~no>

- Only every x-th data-point taken from load history

- Evaluate envelope curve only <1~yes, 0~no>

Solution variable

- Minimum damage – this option is not active for this high-cycle fatigue method

Material parameters

E	[MPa]	tensile modulus
NU	[-]	Poisson’s ratio
TENS0	[MPa]	fatigue limit in repeated tension (or plane bending)
TENS-1	[MPa]	fatigue limit in fully reversed push-pull (or plane bending)
TORS-1	[MPa]	fatigue limit in fully reversed torsion

Result detail variables

Damage fatigue index is computed, not the damage as a reciprocal value to number of cycles or repetitions

FDD1 NCX x-coordinate of the normal line vector of the critical plane

FDD2 NCY y-coordinate of the normal line vector of the critical plane

FDD3 NCZ z-coordinate of the normal line vector of the critical plane

FDD4 ALFA angle between the normal lines to the critical plane and to the free surface

This help file has been generated by the freeware version of HelpNDoc